在实际问题中进行有目的、有针对性的选择要比盲目的选择要好得多,
同时,需要选择最优的或者近似最优的解决方案,
参考[1][2],对优化算法中的常规方法做一个简单总结。
一些参考资料可以关注下面公众号获取
学习资料获取在求解目标函数的极小值的过程中,若对设计变量的取值范围不加限制,称这种最优化问题为无约束优化问题。尽管对于机械的优化设计问题,多数是有约束的,但无约束最优化方法仍然是最优化设计的基本组成部分。因为约束最优化问题可以通过对约束条件的处理,转化为无约束最优化问题来求解。
无约束一维极值问题求解时一般采用一维搜索法,其中方法包括多种。线性搜索包括黄金分割、斐波那契法、牛顿法等、非线性搜索包括抛物线法和三次插值法。本章主要介绍了求解无约束一维极值问题的不同方法。
无约束最优化算法求解无约束最优化问题的方法,有解析法和直接法两类:
(1)解析法就是利用无约束最优化问题中目标函数f(x)的解析表达式和它的解析性质(如函数的一阶导数和二阶导数),给出一种求它的最优解的方法,或一种求近似解的迭代方法。解析法主要有最速下降法、共扼方向法、共辄梯度法、非二次函数的共扼梯度法、牛顿法、拟牛顿法、变尺度法等。
(2)直接法就是在求最优解的过程中,只用到函数的函数值,而不必利用函数的解析性质。直接法也是一种迭代法,迭代步骤简单。当目标函数的表达式十分复杂,或写不出具体表达式时,它就成为了重要的方法。直接法适应面很广,适用于计算机运算。
无约束优化问题的一般形式可描述为
求n维随机变量
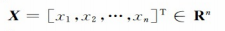
使目标函数f(x)最小。
成功失败法(success-failure method)亦称进退法、倍增半减法,是一种搜索方法,为搜索某区间上函数的极小(大)点,每次搜索都要改变搜索步长的一种方法,如果在第k次迭代沿某方向搜索成功,即函数值下降(上升),下一步仍可沿该方向搜索,而且可以大步向前搜索。
其作法是:从某点t0出发,步长取为λ,若f(t0+λ)<(>)f(t0),则搜索成功,下一步取步长为2λ;
如果第n步的步长为nλ,并搜索成功,下一步取步长为2nλ,若在第k次迭代,沿某方向搜索失败,即函数值上升(下降),则应退回原地,下一步沿相反方向,即向后小步搜索.
其作法是:若f(t0+λ)≥(≤)f(t0),则搜索失败,退回原来点并且再后退λ/4,若第n步步长为nλ,搜索失败,则退回到t0后,还要后退nλ/4.
直到最后搜索步长小于给定的小正数,则停止搜索,得到近似最优点,这里2λ,λ/4都是按经验选取的。
黄金分割法适用于已知极值区间的前提下,利用不断缩小区间的思想,最终得出极值的近似值。该方法只是要求函数单峰,可以不连续。因此,这种方法的适应面非常广泛。
黄金分割法也是建立在区间消去法原理基础上的试探方法,即在搜索区间[a,b]内适当插入两点a1 ,a2 ,并计算其函数值。a1 ,a2将原来区间分成三段,再应用函数的单峰性质,通过函数值大小的比较,删除其中一段,使搜索区间得以缩小。然后在保留下来的区间上作同样的处理,如此迭代下去,使搜索区间无限缩小,从而得到极小值点的数值近似解。
黄金分割法是用于一元函数f(x)在给定的初始区间[a, b]内搜索极小值点a”的一种方法。它是优化计算中的经典算法,以算法简单,收敛速度均匀,效果较好而著称,是许多优化算法的基础。但它只适用于一维区间上的凸函数,即只在单峰区间内才能进行一维寻优,其收敛效率较低。其基本原理是依照去劣存优原则,对称原则以及等比收缩原则来逐步缩小搜索区间。
斐波那契法(Fibonacci Method)又称斐波那契分数法,是一种一维搜索区间消去法。斐波那契法通过取代试探点和进行函数值的比较,使包含极小值点的搜索区间不断缩短,当区间长度缩短到一定程度时,区间上各点的函数值均接近极小值点的近似。该算法要求所考虑的区间上的目标函数是单峰函数,即在这个区间上只有一个局部极小值点的函数。
牛顿型法包括牛顿法和阻尼牛顿法。这类方法的最大优点是收敛速度快,即它的迭代次数相对于其他方法来说少得多。特别是对于一些性态较好的目标函数,例如二次函数,只需保证求梯度和二阶偏导数矩阵时的精度,不管初始点在何处,均可一步就找出最优点。可是这类方法也有很大的缺点,在每次迭代决定牛顿方向时,都要计算目标函数的一阶导数和二阶导数矩阵及其逆矩阵。这就使计算度较为复杂,增加了每次迭代的计算工作量和计算机存储量。
上一节讲了牛顿型法拥有许多良好的性质,如二次收敛速度很快,迭代次数较少,所用存储空间少、程序编写简单等。但不可否认的是,牛顿法仍然存在一些缺点,如局部收敛,需要求函数零点导数等。因此为克服当函数不可导时无法应用牛顿法这一缺点,人们提出了割线法,即
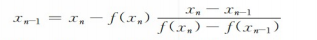
割线法中xn-1计算需要用到xn和xn-1,即需要制定两个初始点。
抛物线法是求无约束一维极值问题的一种方法,也叫二次插值法,其理论依据为二次多项式可以在最优点附近较好地逼近函数的形状,做法是在函数的最优点附近取三个构造点,然后用这三个点构造一条抛物线,把这条抛物线的极值点作为函数的极值点的近似。
每次构造一条抛物线后,抛物线的极值点就可作为一个新的构造点,新的构造点与原来的三个构造点经过某种算法,得到下一步抛物线逼近的三个构造点,这就是抛物线法的算法过程。
在许多问题中,通常根据实验、观测或经验得到的函数表或离散点上的信息,去研究分析函数的有关特性。其中插值法是一种最基本的方法——三次样条插值是三次插值的基本方法
坐标轮换法是将多维问题转化为一系列一维问题的求解方法,它将多变量的优化问题轮流转化为单变量的优化问题,因此又称为变量轮换法。这种方法在搜索过程中只需要目标函数的信息,而不需要求解目标函数的导数。
坐标轮换法轮流沿坐标方向搜索,每次只允许一个变量变化,其余变量保持不变。
在最优化计算中一维最优化方法是优化设计中最简单、最基本的方法。一维极值,又称为线性搜索。一维问题是多维问题的基础,在数值方法迭代计算过程中,都要进行一维极值优化,也可以把多维问题化为一维问题来处理。一维问题算法的好坏,直接影响到最优化问题的求解速度。
约束优化问题的求解可以通过一系列无约束优化方法来达到,所以无约束优化问题的解法是优化设计方法的基本组成部分,也是优化方法的基础。
[1]张岩,吴水根,MATLAB 优化算法. 清华大学出版社, 2017.
[2]高立, 数值最优化方法. 北京大学出版社, 2014.




